Perché la moltiplicazione per gelosia funziona?

In questa fase si continuerà a lavorare sul confronto tra l’uso del diagramma a gelosia e del diagramma rettangolo per il calcolo delle moltiplicazioni. L’obiettivo è di sviluppare, attraverso il confronto tra questi due algoritmi, i significati matematici e i perché che stanno alla base del loro funzionamento – scoprendo e approfondendo le caratteristiche della notazione posizionale decimale e le proprietà della moltiplicazione tra numeri naturali.

Prima di affrontare questa fase consigliamo di visionare i seguenti webinar (disponibili anche alla pagina https://www.percontare.it/webinar/):

Webinar del 14/10/2021 “Discussione e Argomentazione” al link: https://youtu.be/TCPQMwB0MFc
Intervento di Alessandro Ramploud al webinar del 16/02/2021 “Processi di insegnamento-apprendimento della matematica. Guida partica allo stress da procedure” al link: https://youtu.be/merbTiyr0yQ
Intervento di Silvia Funghi del webinar del 25/06/2020 “Nuovi sviluppi del progetto PerContare: la guida per la classe terza” al link: https://youtu.be/twxsAijOrmA?t=3152
Intervento di Alessandro Ramploud al webinar del 05/06/2020 “Didattica della matematica e buone pratiche nel progetto PerContare” al link: https://youtu.be/iTWNw7VzYvI?t=2764
Intervento di Alessandro Ramploud al webinar AperiAIRDM del 06/05/2020 “Argomentando si impara”: https://youtu.be/8KEPB355aS8

Inoltre, per ulteriori approfondimenti, rimandiamo ai seguenti articoli:

Baccaglini-Frank, A., Funghi, S., Maracci, M., & Ramploud, A. (2023). “One times one, but actually they are ten times ten”: Learning about multiplication and decimal notation in third grade by comparing algorithms. The Journal of Mathematical Behavior, 70. ISSN 0732-3123, https://doi.org/10.1016/j.jmathb.2022.101024
Baccaglini-Frank, A., Funghi, S., Maracci, M., & Ramploud, A. (in via di pubblicazione sulla rivista italiana Archimede). A caccia di significati matematici attraverso il confronto: sinergia di algoritmi per la moltiplicazione.
Ramploud, A., Funghi, S. & Baccaglini-Frank, A. (in stampa negli atti del convegno internazionale online 9th ERME Topic Conference: Perspectives on conceptual understanding of flexibility, number sense and mastery in arithmetic, 11-12 Giugno 2021). Meaning making through comparison of multiplication algorithms, an example of task design in the cultural transposition of lesson study.

Materiali e ambientazione/setting

Per ogni gruppo, serviranno:

1 scheda operativa (scheda_diag-gelosia_fase opzionale_perché la gelosia funziona)

Lancio

Si consiglia di svolgere questa qualche tempo dopo il primo confronto realizzato fra il diagramma rettangolo e il diagramma gelosia nella fase precedente. Sarà quindi necessario riprendere quanto emerso in quell’occasione per rilanciare la necessità di approfondire il confronto (p.es. proiettando le differenti soluzioni trovate dai vari gruppo, o le riflessioni fatte in classe durante la discussione, etc.).

Consegna

Vi ricordate cosa avete detto la scorsa volta confrontando il diagramma a gelosia con il diagramma rettangolo? Oggi faremo una cosa molto difficile… da veri matematici. Dobbiamo cercare di capire perché, se moltiplico 2 numeri usando il diagramma rettangolo o il diagramma a gelosia ottengo lo stesso risultato.

Ora vi darò una scheda con una moltiplicazione. Provate a fare il calcolo sia con il diagramma rettangolo, che con il diagramma gelosia. Una volta che avrete terminato, provate a rispondere alle domande che trovate nella scheda. Alla fine di questo lavoro ci confronteremo.

L’insegnante consegnerà quindi ad ogni gruppo la scheda operativa (scheda_diag-gelosia_fase opzionale_perché la gelosia funziona) in cui viene richiesto di svolgere la stessa moltiplicazione, 12 x 14, sia con il diagramma rettangolo che con il diagramma a gelosia (si veda la Figura 1).

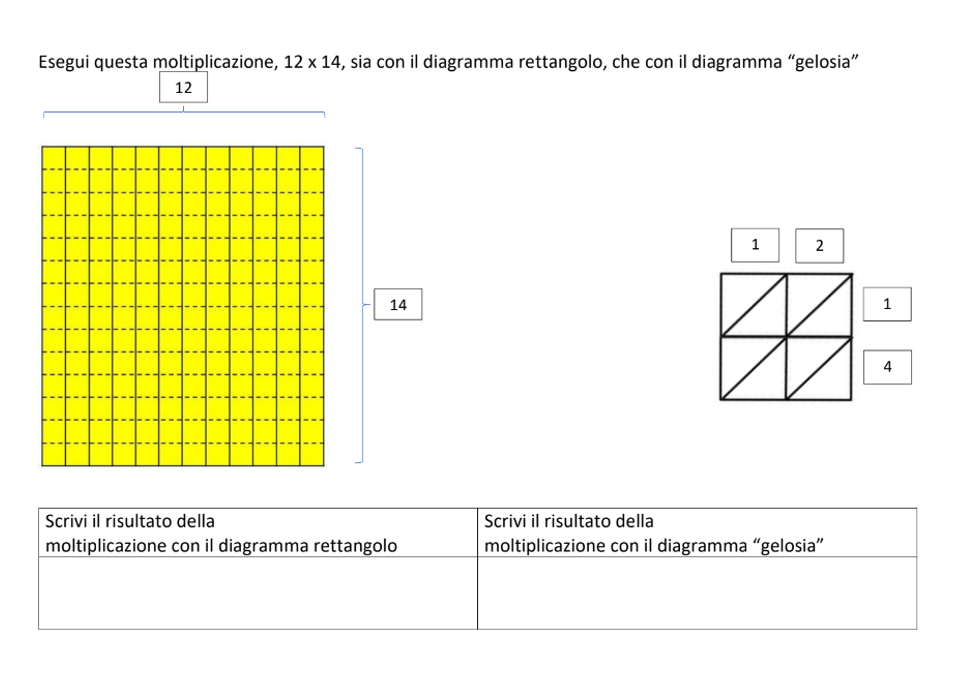
Figura 1: Compito riportato sulla prima pagina della scheda operativa.

Se fino a quel momento la classe ha utilizzato uno dei due algoritmi con delle modalità diverse, l’insegnante potrà porre in discussione con i bambini e le bambine su come funzionano i due diagrammi a gelosia nel caso proposto dalla scheda operativa (p.es. chiedendo “Il diagramma rettangolo che vi darò non ha i numeri da moltiplicare scritti uno sotto e uno a sinistra, ma uno a destra e uno in alto; secondo voi cambia qualcosa?”). In particolare, nel caso in cui fino a questo momento la classe abbia utilizzato il diagramma a gelosia sempre “in verticale” (si veda la sezione “Introduzione, una nota storica” nella pagina https://www.percontare.it/guide/classe-terza/diagramma-gelosia/), l’insegnante potrà porre in discussione con i bambini e le bambine su come funziona il diagramma a gelosia nel caso proposto dalla scheda operativa (p.es. dicendo: “Il diagramma a gelosia in questo caso non è messo come lo usiamo di solito, come funziona secondo voi in questo caso?”).

Nel secondo foglio della scheda operativa sono riportate le seguenti due domande:

Cosa notate?
Cercate di spiegare le ragioni di ciò che avete osservato.

Esplorazione

I gruppi cominciano a lavorare per calcolare la moltiplicazione proposta eseguendo i due algoritmi e compilando la scheda.

Anche se non viene richiesto esplicitamente agli studenti di scomporre il diagramma rettangolo secondo la scomposizione 12=10+2 e 14=10+4, ci aspettiamo che alcuni studenti possano individuare questo approccio come quello più utile in questo caso per operare il confronto con il diagramma a gelosia (si veda la Figura 2), anche data l’esperienza precedente con i diagrammi rettangolo (si veda la fase https://www.percontare.it/guide/classe-terza/diagramma-rettangolo/diagramma-rettangolo-fase-2). Tuttavia, ci aspettiamo anche che i bambini e le bambine possano proporre altre scomposizioni dei fattori 12 e 14 (ad esempio, 12=5+5+2, 14=10+4, ecc.), in base alle loro preferenze personali e alla loro conoscenza di fatti moltiplicativi. In tal caso, la scelta di scomposizioni diverse da quella 12=10+2 e 14=10+4 potrebbe portare a costruire delle corrispondenze tra i due algoritmi possibilmente diverse da quelle descritte qui nel seguito. L’insegnante per il momento accoglierà tutte le osservazioni e tutte le corrispondenze individuate dai bambini e dalle bambine, che verranno poi messe al centro della parte di discussione.

Figura 2: Esempio di protocollo compilato da un gruppo di una delle classi sperimentali.

ATTENZIONE: L’approccio per scomposizione canonica dei fattori è l’approccio che in questa consegna è probabilmente quello preferibile per operare un confronto, ma non è detto che sia sempre così. In particolare, non stiamo cercando di portare i bambini a preferire sempre la scomposizione canonica rispetto alle altre scomposizioni, ma di favorire la loro consapevolezza delle proprietà intrinseche dei numeri quando sono scritti nella notazione posizionale in base dieci. In questa prospettiva, sarà particolarmente importante permettere ai bambini e alle bambine di scegliere l’approccio alla scomposizione del diagramma rettangolo più congeniale per loro, e dedicare parte della discussione alla funzionalità di diverse scomposizioni in relazione al compito dato.

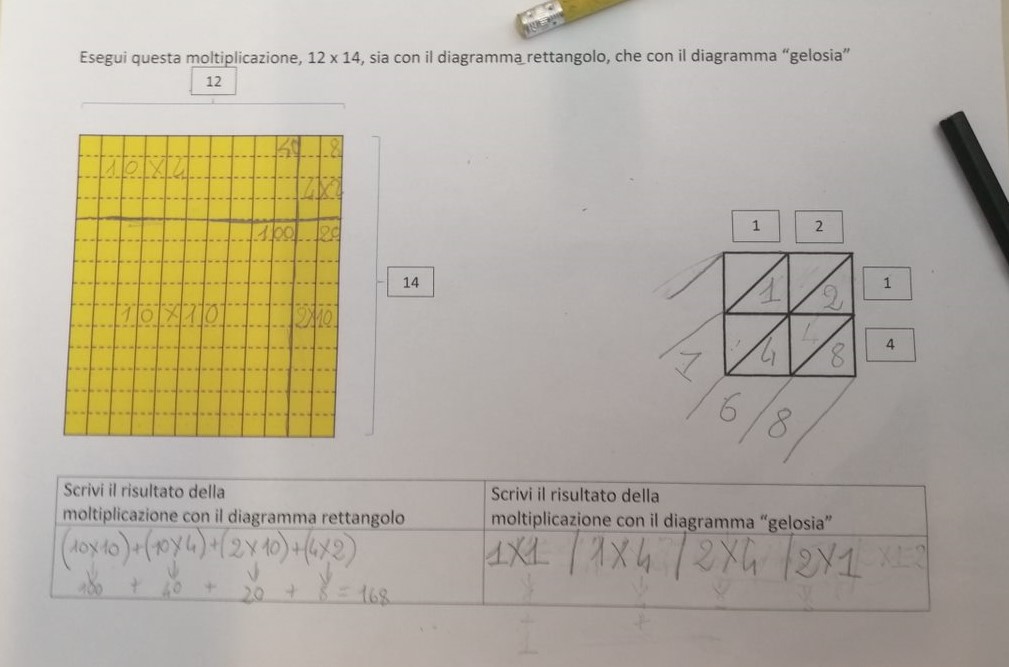
L’osservazione dell’insegnante sarà incentrata su segni (p.es. parole, gesti, disegni, etc.) utilizzati dai bambini e dalle bambine per esprimere somiglianze e differenze tra i due algoritmi. In particolare, sarà estremamente importante individuare segni (p.es. espressioni come “questo è uguale a quello”) che possano indicare un processo di costruzione di corrispondenze tra i sottorettangoli nel diagramma rettangolo e i prodotti parziali all’interno del diagramma a gelosia (p.es. “abbiamo calcolato 2×4=8 sia di qua che di là, solo che nel diagramma rettangolo quello è un palazzo mentre nella gelosia è un numero”, “qui nella gelosia facciamo 1×1 ma facciamo 10×10 nel diagramma rettangolo”). Altrettanto importante sarà l’attenzione ad eventuali commenti da parte dei bambini e delle bambine sul fatto che i due algoritmi producono lo stesso prodotto finale, ma attraverso percorsi diversi, o che mettano in relazione segni matematici conosciuti con il funzionamento (di almeno uno) dei due algoritmi (p.es. “Le cifre sono le stesse, sono come due macchine diverse che calcolano la stessa cosa”; “In entrambi i casi spezzi i due numeri, solo che lo fai in modo diverso”- si veda anche la figura a seguire dove i bambini e le bambine scrivono che “nella gelosia i numeri sono già scritti spaccati in decine e unità“).

Figura 3: Esempio di protocollo compilato da un gruppo di una delle classi sperimentali. I bambini in risposta alla prima domanda scrivono: “Noi abbiamo notato che il risultato non cambia perché le cifre sono le stesse, anche i prodotti parziali sono uguali perché si trovano sulla gelosia gli stessi risultati* (* es. 20 nel diagramma rettangolo). Il diagramma a gelosia è sempre lo stesso, 100 nel diagramma a gelosia unisco lo 0 e il 1 poi quello del 8 e ci viene 100, 40 nel diagramma rettangolo invece quello a gelosia mischio 0 e 4”. In risposta alla seconda domanda scrivono “Perché nella gelosia i numeri sono già scritti spaccati in decine e unità“. In questo protocollo descrive alcuni elementi interessanti del processo di scoperta delle relazioni tra i due algoritmi che sta avvenendo: da un lato la risposta alla prima domanda ci fa pensare che i bambini abbiano messo in relazione i due algoritmi andando a cercare dentro la gelosia le cifre che compongono i prodotti parziali del diagramma rettangolo in ordine sparso, in modo quindi non collegato con la scomposizione dei fattori; d’altro canto, la risposta alla seconda domanda ci mostra però che forse i bambini e le bambine abbiano riconosciuto che nella moltiplicazione con diagramma a gelosia la scomposizione dei fattori sia in qualche modo “obbligata” rispetto all’ordine posizionale delle cifre dei due fattori. Questi elementi, per quanto ancora in una forma non raffinata da un punto di vista matematici, sono elementi molti preziosi per l’argomentazione che si può andare a costruire in fase di discussione.

Discussione

Un portavoce per ogni gruppo dirà quale risultato della moltiplicazione 12×14 hanno trovato, se hanno ottenuto lo stesso risultato con i due algoritmi, e leggerà le riflessioni svolte. Qui l’insegnante dovrà prestare particolare attenzione a ciò che i portavoce dicono e evidenziare gli elementi funzionali a sviluppare l’attenzione su somiglianze e differenze dei due algoritmi (p.es. con espressioni del tipo “le due moltiplicazioni sono uguali, però una è più grande e l’altra è più piccola”), in particolare in relazione ai possibili modi di scomporre i due fattori 12 e 14 (p.es. facendo attenzione all’emergere di parole come “spaccare” – si veda p.es. il video a seguire – o di segni matematici come “decine” o “unità” per parlare della scomposizione dei fattori).

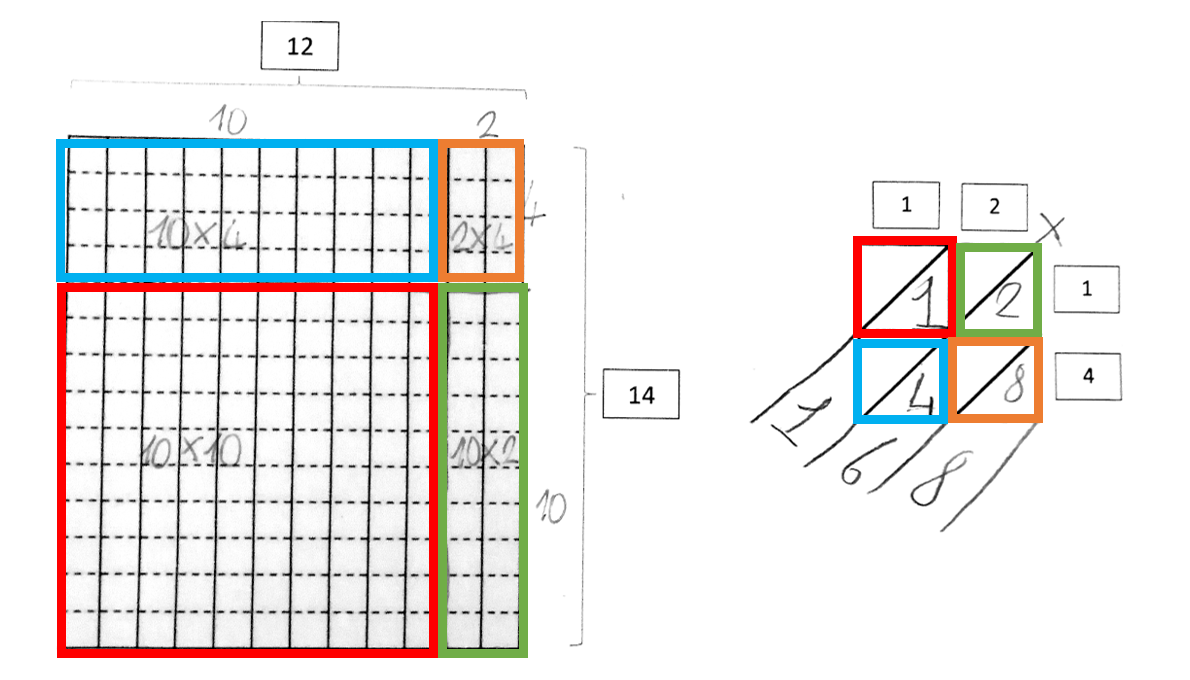
Altro punto molto importante da attenzionare riguarda le espressioni utilizzate dai bambini e dalle bambine per associare i sottorettangoli del diagramma rettangolo con i prodotti parziali contenuti nel diagramma a gelosia (p.es. “questo 1 in realtà vale 10”, “nella gelosia non ci accorgiamo che non mettiamo gli zeri”, etc.). Potrebbe infatti accadere che tra i gruppi che hanno scelto di dividere il diagramma rettangolo scomponendo i fattori come 12=10+2 e 14=10+4, qualcuno faccia una o più delle seguenti associazioni (si vedano per esempio il video e la Figura a seguire):

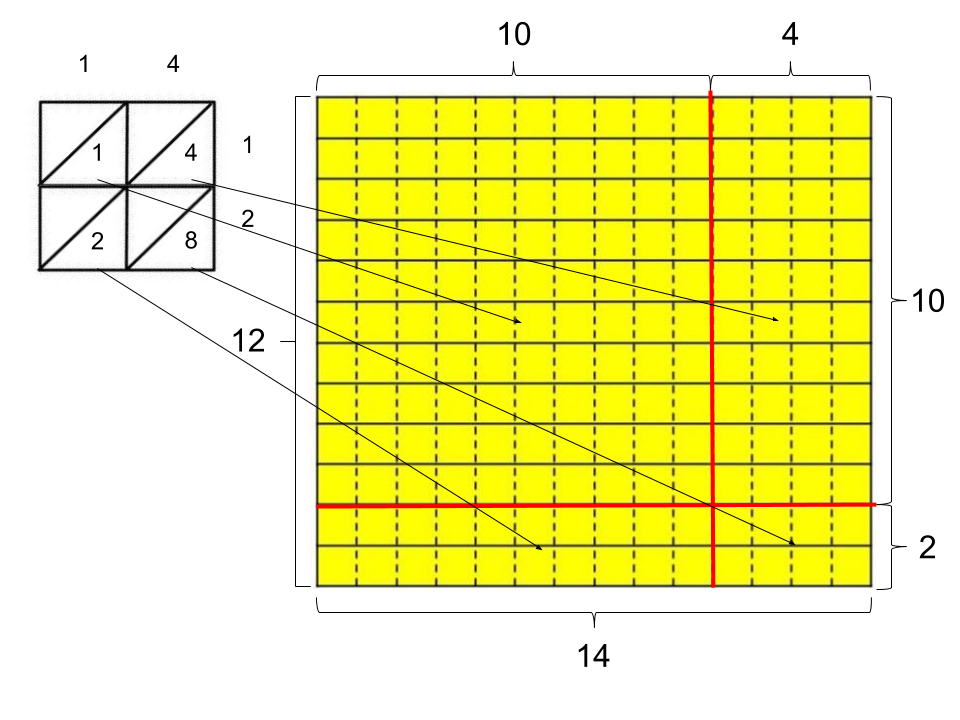
moltiplicando l’1 al posto delle decine del 12 con l’1 al posto delle decine del 14 si ottiene l’1 che compare nel riquadro in alto a sinistra del diagramma a gelosia. Questo 1 corrisponde al sottorettangolo 10×10 del diagramma rettangolo;
il 2 e il 4 nei riquadri del diagramma a gelosia, che si ottengono moltiplicando l’1 al posto delle decine di uno dei due fattori con la cifra al posto delle unità dell’altro fattore, corrispondono ai sottorettangoli 2×10 e 10×4 del diagramma rettangolo;
l’8 che compare nel riquadro in alto a sinistra del diagramma a gelosia, che si ottengono moltiplicando il 2 al posto delle unità del 12 e il 4 al posto delle unità del 14, corrisponde alle 8 unità del sottorettangolo 2×4 del diagramma rettangolo.

Figura 4: Scheda operativa a cui fa riferimento la bambina nel video precedente. Sono evidenziati nello stesso colore i sottorettangoli del diagramma rettangolo e le celle del diagramma a gelosia che vengono messi in corrispondenza dalla bambina nel video.

Sarà estremamente importante, in questo passaggio, chiedere sempre agli altri gruppi cosa ne pensano, se sono d’accordo o meno con quanto presentato dal portavoce, etc. : l’intento, infatti, è quello di portare l’attenzione degli studenti sul fatto che le due procedure portino al medesimo risultato ma con procedimenti differenti. Nel diagramma rettangolo, infatti, i passaggi della procedura corrispondono in modo molto trasparente con la scomposizione dei due fattori e il calcolo dei prodotti parziali dal punto di vista matematico (si tratta di una applicazione informale e visiva della proprietà distributiva della moltiplicazione rispetto all’addizione); nel diagramma a gelosia, invece, è molto meno immediato risalire a quali siano i significati matematici dietro ai singoli passaggi della procedura, quindi in questo senso risulta essere un algoritmo più “opaco” rispetto al diagramma rettangolo. La riflessione sulle corrispondenze individuate, quindi, sarà fondamentale per rendere espliciti questi significati matematici che rimangono “opachi” nel diagramma a gelosia (si veda il video a seguire dove uno studente cerca di spiegare un aspetto di “opacità” del diagramma a gelosia, che riguarda l’ordine di grandezza delle cifre che compaiono all’interno del diagramma).

Il confronto tra i due algoritmi, quindi, sarà volto a permettere ai bambini e alle bambine di co-costruire una vera a propria argomentazione sul perché la moltiplicazione per gelosia funziona, andando a dare ad ogni cella della gelosia un significato più trasparente proprio grazie al confronto. Si veda il video a seguire per avere un esempio preso da alcuni esperimenti nelle classi sperimentali di come si possa co-costruire una argomentazione di questo genere all’interno della discussione di classe.

Se dal lavoro di tutti i gruppi e dalla discussione non fosse ancora emersa la possibilità di scomporre il diagramma rettangolo secondo la notazione posizionale decimale dei due fattori (cioè 12=10+2 e 14=10+4), l’insegnante potrà rilanciare la seguente consegna.

Consegna 2

Siete stati davvero bravi, avete detto delle cose molto importanti, però vorrei chiedervi di fare un’altra cosa. Siete molto bravi a scrivere i numeri in modi differenti, per es. 42 può essere scritto anche come 4 da e 2 u. Adesso vi darò un’altra scheda dove dovrete provare a fare questo esercizio. Una volta fatto provate a rispondere alle domande.

L’insegnante consegnerà quindi la scheda operativa opzionale scheda opzionale_diag-gelosia_fase opzionale_perché la gelosia funziona su cui i gruppi dovrebbero cominciare a riflettere. Una volta terminata la compilazione anche di questa seconda scheda operativa si potrà ritornare alla discussione.

Conclusioni

L’insegnante, a questo punto, dovrà sottolineare, avvalendosi di un cartellone/lavagna, LIM… per fare sintesi del lavoro, le riflessioni scaturite dai bambini e dalle bambine su possibili relazioni tra i due algoritmi e gli argomenti (anche parziali o ancora situati) emersi per costruire una argomentazione del funzionamento delle due procedure di moltiplicazione. Sarà importantissimo far costruire una documentazione, anche sul quaderno dei bambini, relativa ad alcune parole che si ritengono significative per la descrizione delle procedure d’utilizzo dell’algoritmo.

Se emerso all’interno della discussione, l’insegnante potrà sottolineare come la scomposizione canonica dei fattori in questo compito sia diventata la scelta ottimale per consentire un confronto passo-passo dei due algoritmi, mentre nelle precedenti esperienze con la moltiplicazione per diagramma rettangolo era solo una possibilità tra le tante (si veda https://www.percontare.it/guide/classe-terza/diagramma-rettangolo/diagramma-rettangolo-fase-2). Particolare attenzione andrà posta alle relazioni che sono state individuate dai bambini e dalle bambine tra i segni all’interno dei due algoritmi, come per esempio:

corrispondenza dell’1 del diagramma a gelosia al 100 (o all’1 h) del diagramma rettangolo (si veda la Figura 5);
dipendenza, in modi diversi, dei due algoritmi dalla notazione posizionale decimale delle cifre dei fattori;
diversa rappresentazione dei prodotti parziali nei due algoritmi;
etc.

L’insegnante cercherà quindi di mettere in evidenza come entrambi gli algoritmi rimandino agli stessi significati matematici, ma differiscano in modo significativo dal punto di vista della “trasparenza” (il diagramma rettangolo rende visibile il significato della moltiplicazione, mentre nel diagramma a gelosia vi è una continua opacizzazione del significato a vantaggio di una proceduralizzazione).

Figura 5: Corrispondenze tra i prodotti parziali all’interno del diagramma a gelosia e i sottorettangoli nel diagramma rettangolo scomposto secondo la notazione posizionale decimale dei due fattori 12 e 14.

Proposte di consolidamento

In lezioni successive a quella in cui si realizza la presente attività si può dedicare attenzione alla costruzione di una vera e propria argomentazione – in forma scritta – del motivo per cui il calcolo della moltiplicazione 12×14 con i due algoritmi porta allo stesso risultato. Si può per esempio partire dalla stesura di una prima spiegazione che raccolga le osservazioni degli studenti e dei motivi per cui loro sostengono un certo punto di vista, anche in modo non collegato tra loro. Si potrà andare poi a lavorare sulla stesura di un testo più coeso che nel suo complesso fornisca una giustificazione del perché la moltiplicazione per gelosia 12×14 funziona, alla luce di quanto scoperto grazie al diagramma rettangolo, mantenendo ancora i segni situati introdotti dagli studenti. Infine, si potrà limare ulteriormente il testo fin qui costruito andando ad introdurre dei veri e propri segni matematici che possono riassumere quello che fin qui è stato descritto un modo situato (p.es. il termine “spaccare” riferito ai fattori 12 e 14, utilizzato dagli studenti nei video precedenti può essere sostituito dal termine specifico “scomporre”).

Copione da stampare per l’insegnante

Quello che riportiamo nel seguito è una scheda di progettazione diversa da quella utilizzata per il copione delle altre attività del progetto PerContare, in quanto il lavoro presentato in questa fase opzionale è frutto di un esperimento di Lesson Study realizzato dal team di PerContare insieme a vari team di insegnanti (per approfondimenti sul Lesson Study rimandiamo al libro: Il Lesson Study per la formazione insegnanti (2018), a cura di Bartolini Bussi & Ramploud, edito da Carocci).

pianificazione della lezione diagramma rettangolo-diagramma gelosia