Durata: 1 ora
Preparazione e Consegna
L’insegnante disegna alla lavagna la rappresentazione seguente, oppure consegna a tutti i bambini una fotocopia che la contiene.
3 per 2 volte
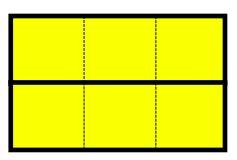
L’insegnante da’ la seguente consegna:
Osserva la rappresentazione di “3 per 2 volte” che usa le barrette con tacche.
Descrivi la rappresentazione con parole tue
Rappresenta di fianco “2 per 3 volte”.
Confronta le rappresentazioni. Di quanti quadratini sono composti in tutto? Quali differenze noti tra le due rappresentazioni?
Senza rifare il disegno, come potresti guardare la rappresentazione di “3 per 2 volte” per vederla come quella di “2 per 3 volte”?
Che cosa aspettarsi
Questa è la prima attività con cui la nuova rappresentazione viene introdotta. I bambini avranno bisogno di appropriarsene e di prendere dimestichezza con la terminologia che proponiamo di associarvi. In particolare, potrebbe essere che in un primo momento non tutti concordino sull’usare le parole “3 per 2 volte” associate all’immagine, perché potrebbero interpretarla verbalmente in modi diversi. È importante, invece, arrivare ad argomentazioni su perché la figura potrebbe rappresentare proprio quelle parole.
Significati matematici che si vogliono costruire
In questa fase si mira a stabilire un legame tra un’espressione verbale ed un’immagine, date entrambe, perché possiedono un grande potenziale semiotico. In particolare, verbalmente, stiamo usando l’espressione: “[un numero] per [un numero di] volte” riferendoci ad un’immagine che può essere vista come una ripetizione di un numero rappresentato come una successione orizzontale di quadrati. Stiamo gettando i semi per far emergere significati della moltiplicazione usando il codice visivo analogico e quello verbale. In questa attività stiamo favorendo lo sviluppo di abilità di transcodifica tra questi codici. La domanda b) propone una variazione della descrizione verbale della rappresentazione e chiede al bambino di fornire la corrispondente variazione visiva, un rettangolo simmetrico rispetto al primo (lungo una linea obliqua inclinata di 45 gradi rispetto alla base del rettangolo rappresentato) oppure ruotato di 90 gradi rispetto al primo. Le domande successive mirano a stabilire analogie e differenze tra le rappresentazioni di “3 volte 2” e “2 volte 3”.
Come costruire i significati matematici
È importante far parlare il maggior numero di bambini possibile, in modo che le loro idee vengano esplicitate e messe a confronto, per poterle poi far convergere su alcune convenzioni. Per esempio:
- La rappresentazione del diagramma-rettangolo (chiamarlo come propongono i bambini) è costituito da una fila in basso che rappresenta un numero da ripetere, in altezza, quante volte dice la parte “…per [numero] volte”, che potrebbe essere letto anche come “ripetuto per [numero] volte.”
- Le rappresentazioni dei diagrammi-rettangolo in cui sono scambiati i numeri sono composti dello stesso numero di quadretti; questi numeri si possono ottenere sommando il numero ripetuto quante volte dice “…per [numero] volte” nell’espressione verbale.
- Le rappresentazioni dei diagrammi-rettangolo in cui sono scambiati i numeri si possono ottenere l’uno dall’altro con una rotazione o una simmetria assiale (non si userà questa terminologia, ma è possibile che alcuni bambini menzionino una sorta di specularità o simmetria, soprattutto se hanno svolto le attività proposte su questa trasformazione.
In questo video un bambino rappresenta il rettangolo “4 per 3 volte”. Disegna ciascun quadretto componente singolarmente. Questo è indice di una percezione di struttura ancora non avanzata perchè probabilmente il bambino non + riuscito a immaginarsi il rettangolo come griglia con una data altezza e larghezza, ma come insieme di quadretti. In ogni caso rappresenta i quadretti nella corretta relazione reciproca, usando la quadrettatura del foglio appeso.
Altre schede-esempio e possibili compiti
Proponiamo di inventare altre descrizioni a parole di possibili diagrammi-rettangolo e di far costruire questi ai bambini, insieme alle rappresentazioni simmetriche; indichiamo alcuni esempi di schede per esercizi.
